How to Read a Syntax Tree While Loop
As I promised you last time, today I will talk about one of the central data structures that we'll use throughout the rest of the series, so buckle up and let's get.
Up until now, we had our interpreter and parser lawmaking mixed together and the interpreter would evaluate an expression every bit before long equally the parser recognized a certain language construct similar addition, subtraction, multiplication, or division. Such interpreters are called syntax-directed interpreters. They unremarkably make a unmarried pass over the input and are suitable for basic language applications. In guild to analyze more than complex Pascal programming language constructs, we need to build an intermediate representation ( IR ). Our parser will be responsible for building an IR and our interpreter volition utilise it to interpret the input represented as the IR .
Information technology turns out that a tree is a very suitable data structure for an IR.
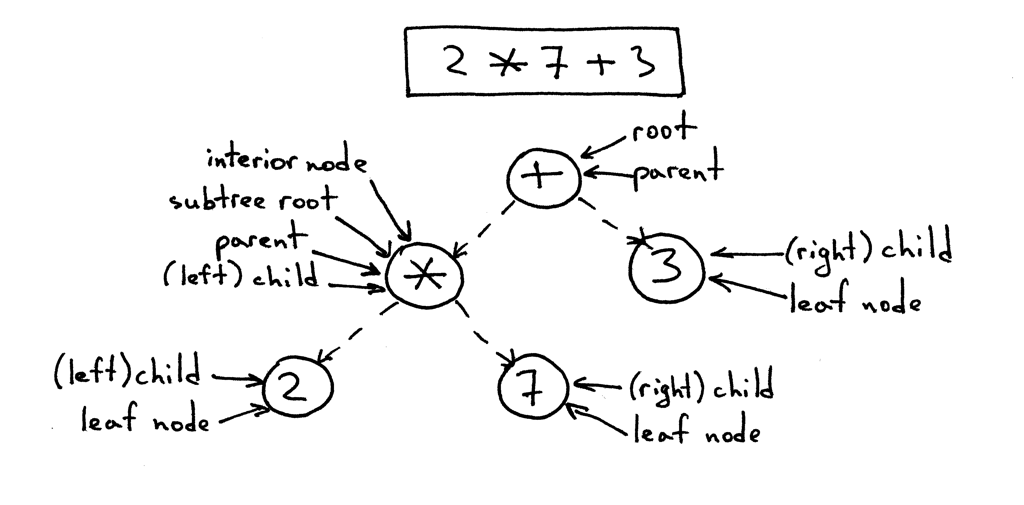
Allow's chop-chop talk about tree terminology.
- A tree is a data construction that consists of i or more than nodes organized into a hierarchy.
- The tree has 1 root, which is the top node.
- All nodes except the root have a unique parent.
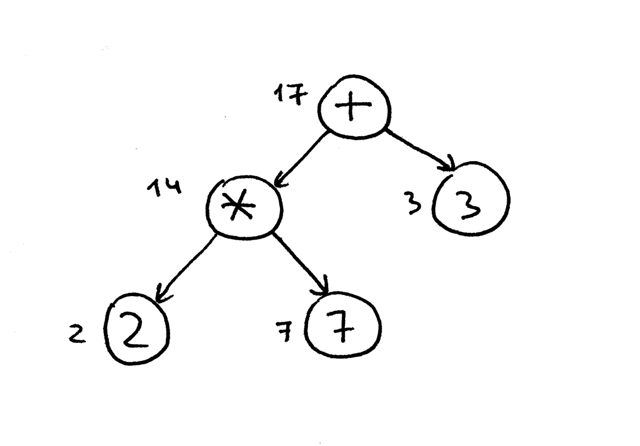
- The node labeled * in the picture below is a parent. Nodes labeled 2 and seven are its children; children are ordered from left to right.
- A node with no children is called a leaf node.
- A node that has i or more children and that is not the root is called an interior node.
- The children can too be complete subtrees. In the picture below the left child (labeled *) of the + node is a complete subtree with its own children.
- In computer science we draw copse upside down starting with the root node at the pinnacle and branches growing downward.
Here is a tree for the expression 2 * 7 + three with explanations:
The IR we'll use throughout the series is called an abstruse-syntax tree ( AST ). But before we dig deeper into ASTs allow'southward talk about parse copse briefly. Though we're not going to utilise parse trees for our interpreter and compiler, they can help you understand how your parser interpreted the input by visualizing the execution trace of the parser. Nosotros'll also compare them with ASTs to meet why ASTs are better suited for intermediate representation than parse trees.
So, what is a parse tree? A parse-tree (sometimes chosen a concrete syntax tree) is a tree that represents the syntactic structure of a linguistic communication construct co-ordinate to our grammar definition. It basically shows how your parser recognized the language construct or, in other words, it shows how the start symbol of your grammar derives a certain cord in the programming language.
The call stack of the parser implicitly represents a parse tree and it's automatically built in memory by your parser every bit it is trying to recognize a certain language construct.
Let'southward take a look at a parse tree for the expression 2 * 7 + 3:
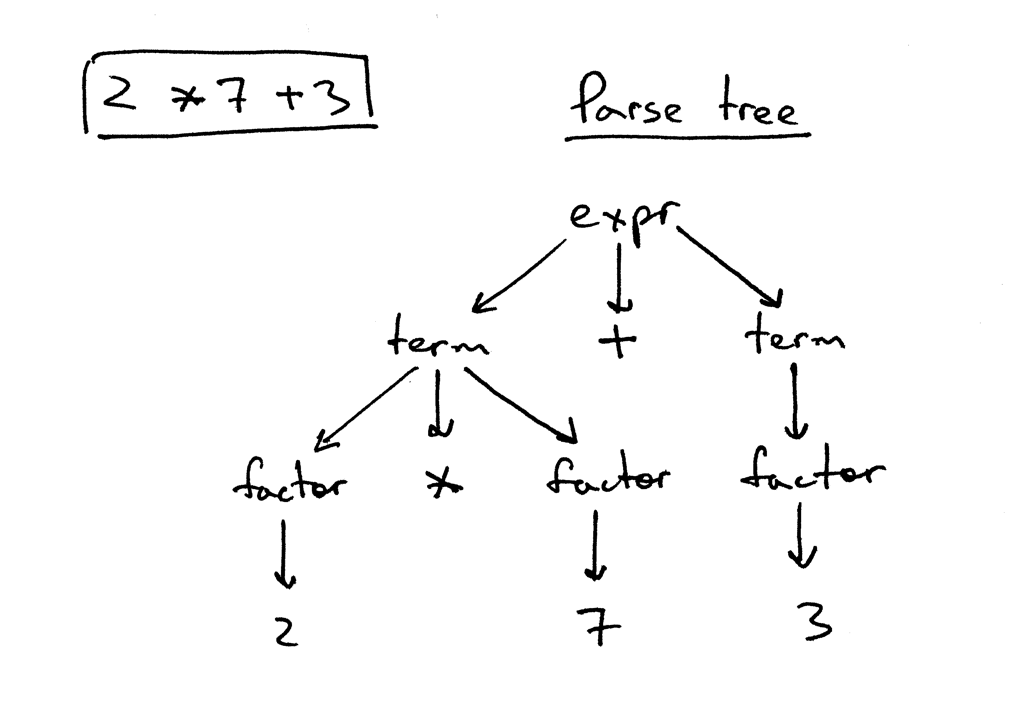
In the moving-picture show higher up y'all can see that:
- The parse tree records a sequence of rules the parser applies to recognize the input.
- The root of the parse tree is labeled with the grammar start symbol.
- Each interior node represents a not-terminal, that is it represents a grammer dominion application, like expr, term, or factor in our case.
- Each foliage node represents a token.
As I've already mentioned, we're not going to manually construct parser trees and use them for our interpreter but parse trees can assistance you understand how the parser interpreted the input past visualizing the parser call sequence.
You lot can see how parse trees look similar for unlike arithmetic expressions by trying out a small utility called genptdot.py that I quickly wrote to help you visualize them. To utilize the utility you first need to install Graphviz package and afterwards you've run the post-obit command, you can open the generated image file parsetree.png and see a parse tree for the expression you lot passed as a command line argument:
$ python genptdot.py "fourteen + two * 3 - 6 / 2" > \ parsetree.dot && dot -Tpng -o parsetree.png parsetree.dot Here is the generated image parsetree.png for the expression 14 + two * 3 - 6 / two:
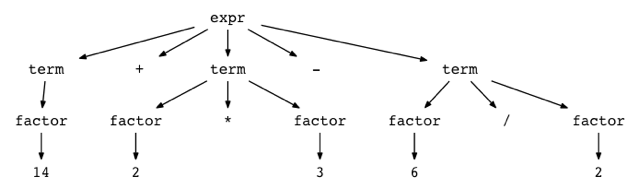
Play with the utility a fleck by passing information technology different arithmetic expressions and encounter what a parse tree looks like for a particular expression.
Now, permit's talk virtually abstract-syntax trees (AST). This is the intermediate representation (IR) that we'll heavily use throughout the balance of the series. It is one of the central data structures for our interpreter and future compiler projects.
Let's start our discussion by taking a look at both the AST and the parse tree for the expression two * vii + 3:
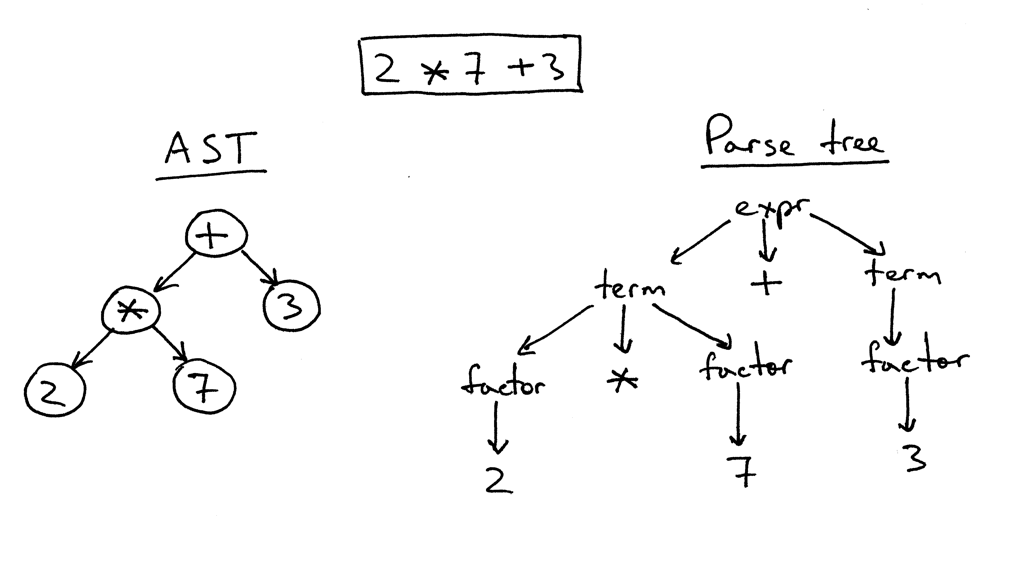
As you tin see from the picture above, the AST captures the essence of the input while beingness smaller.
Here are the main differences betwixt ASTs and Parse trees:
- ASTs uses operators/operations every bit root and interior nodes and it uses operands as their children.
- ASTs do not apply interior nodes to represent a grammar dominion, unlike the parse tree does.
- ASTs don't represent every detail from the real syntax (that's why they're called abstract) - no dominion nodes and no parentheses, for instance.
- ASTs are dense compared to a parse tree for the same linguistic communication construct.
So, what is an abstract syntax tree? An abstract syntax tree ( AST ) is a tree that represents the abstract syntactic structure of a linguistic communication construct where each interior node and the root node represents an operator, and the children of the node stand for the operands of that operator.
I've already mentioned that ASTs are more meaty than parse trees. Allow'due south have a look at an AST and a parse tree for the expression seven + ((2 + 3)). You tin come across that the following AST is much smaller than the parse tree, merely even so captures the essence of the input:
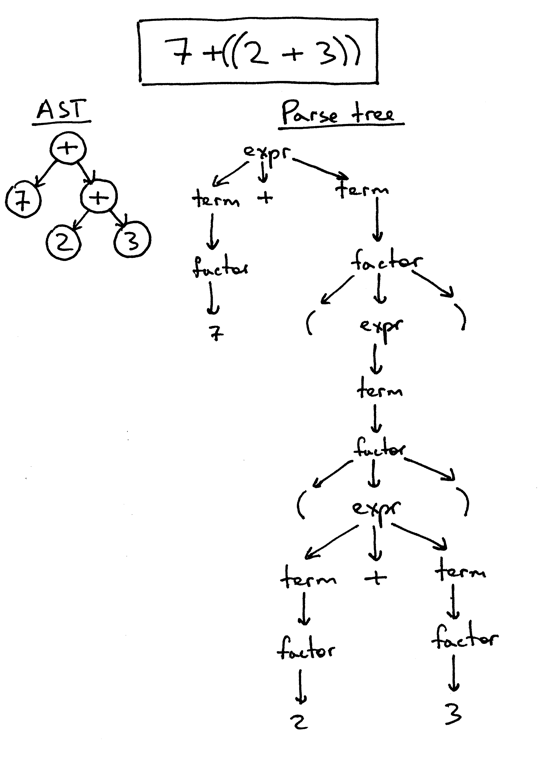
So far so expert, but how do you lot encode operator precedence in an AST? In guild to encode the operator precedence in AST, that is, to represent that "X happens earlier Y" you just need to put Ten lower in the tree than Y. And you've already seen that in the previous pictures.
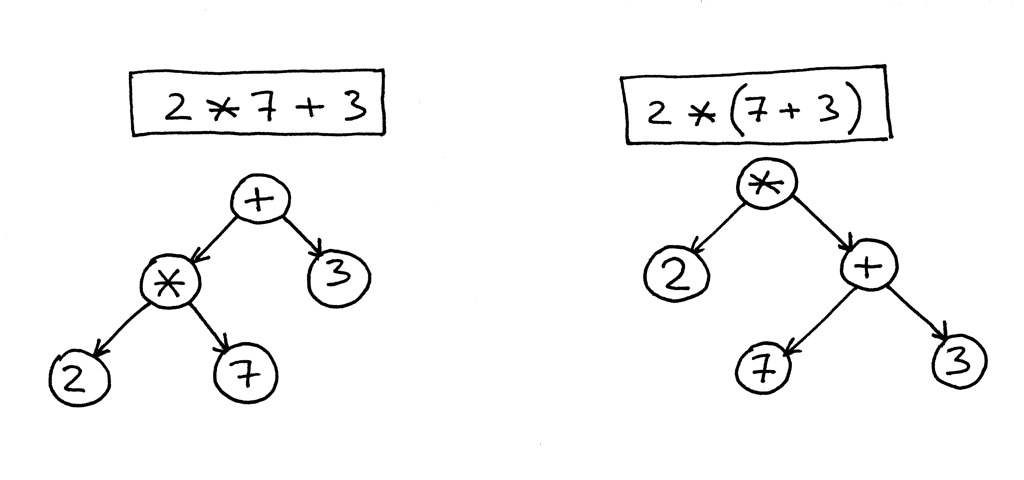
Permit's take a look at some more examples.
In the picture beneath, on the left, you lot can run into an AST for the expression ii * 7 + 3. Let's change the precedence by putting seven + three inside the parentheses. You tin run across, on the correct, what an AST looks like for the modified expression 2 * (7 + 3):
Here is an AST for the expression 1 + 2 + 3 + 4 + five:
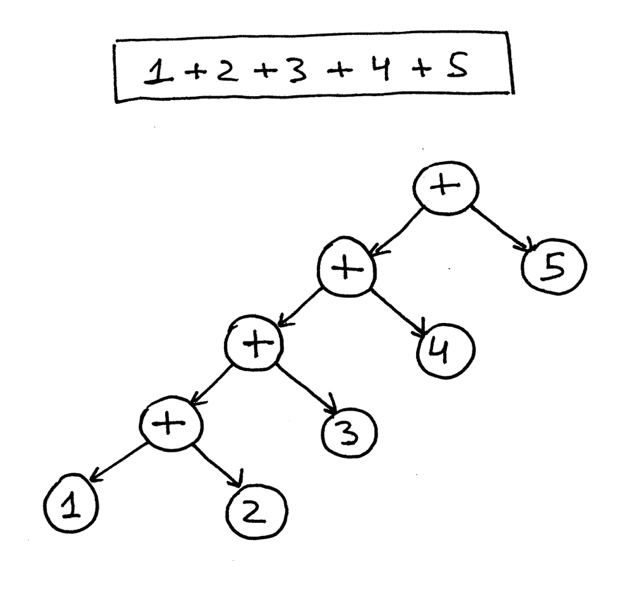
From the pictures above yous can see that operators with higher precedence end upward being lower in the tree.
Okay, allow'south write some code to implement different AST node types and alter our parser to generate an AST tree composed of those nodes.
First, we'll create a base of operations node class chosen AST that other classes will inherit from:
Non much there, actually. Call back that ASTs represent the operator-operand model. And then far, nosotros have four operators and integer operands. The operators are add-on, subtraction, multiplication, and sectionalization. We could have created a separate grade to represent each operator like AddNode, SubNode, MulNode, and DivNode, just instead we're going to have only 1 BinOp class to represent all four binary operators (a binary operator is an operator that operates on two operands):
class BinOp ( AST ): def __init__ ( cocky , left , op , right ): cocky . left = left cocky . token = self . op = op self . right = right The parameters to the constructor are left, op, and right, where left and right point correspondingly to the node of the left operand and to the node of the correct operand. Op holds a token for the operator itself: Token(PLUS, '+') for the plus operator, Token(MINUS, '-') for the minus operator, and so on.
To represent integers in our AST, we'll ascertain a class Num that will hold an INTEGER token and the token's value:
class Num ( AST ): def __init__ ( cocky , token ): cocky . token = token self . value = token . value Equally you've noticed, all nodes store the token used to create the node. This is mostly for convenience and it will come up in handy in the futurity.
Recall the AST for the expression 2 * 7 + 3. We're going to manually create information technology in code for that expression:
>>> from spi import Token , MUL , PLUS , INTEGER , Num , BinOp >>> >>> mul_token = Token ( MUL , '*' ) >>> plus_token = Token ( PLUS , '+' ) >>> mul_node = BinOp ( ... left = Num ( Token ( INTEGER , 2 )), ... op = mul_token , ... right = Num ( Token ( INTEGER , 7 )) ... ) >>> add_node = BinOp ( ... left = mul_node , ... op = plus_token , ... correct = Num ( Token ( INTEGER , 3 )) ... ) Here is how an AST volition look with our new node classes defined. The picture below likewise follows the manual construction procedure above:
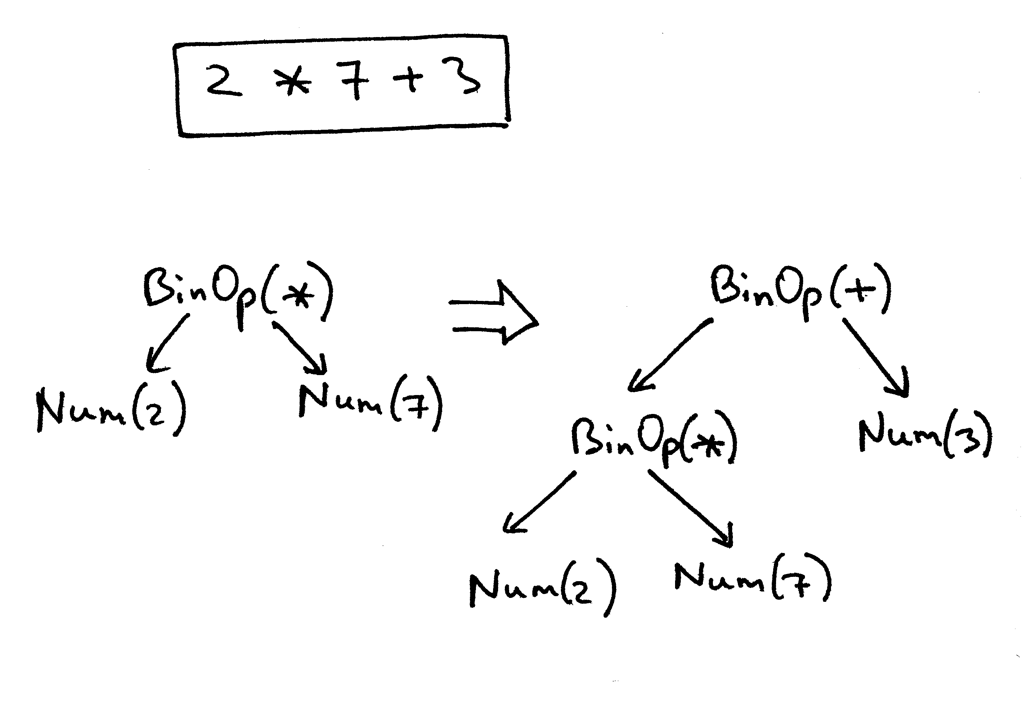
Here is our modified parser code that builds and returns an AST as a consequence of recognizing the input (an arithmetic expression):
class AST ( object ): pass form BinOp ( AST ): def __init__ ( self , left , op , right ): self . left = left self . token = self . op = op self . right = right class Num ( AST ): def __init__ ( self , token ): self . token = token cocky . value = token . value class Parser ( object ): def __init__ ( cocky , lexer ): self . lexer = lexer # set up current token to the first token taken from the input self . current_token = self . lexer . get_next_token () def fault ( cocky ): raise Exception ( 'Invalid syntax' ) def eat ( self , token_type ): # compare the electric current token type with the passed token # blazon and if they lucifer and then "eat" the electric current token # and assign the next token to the cocky.current_token, # otherwise enhance an exception. if self . current_token . type == token_type : cocky . current_token = self . lexer . get_next_token () else : self . error () def gene ( self ): """factor : INTEGER | LPAREN expr RPAREN""" token = self . current_token if token . type == INTEGER : self . eat ( INTEGER ) return Num ( token ) elif token . type == LPAREN : self . swallow ( LPAREN ) node = self . expr () self . consume ( RPAREN ) return node def term ( self ): """term : factor ((MUL | DIV) factor)*""" node = self . gene () while self . current_token . type in ( MUL , DIV ): token = cocky . current_token if token . type == MUL : self . eat ( MUL ) elif token . type == DIV : self . eat ( DIV ) node = BinOp ( left = node , op = token , right = cocky . gene ()) return node def expr ( self ): """ expr : term ((PLUS | MINUS) term)* term : factor ((MUL | DIV) factor)* gene : INTEGER | LPAREN expr RPAREN """ node = self . term () while self . current_token . type in ( PLUS , MINUS ): token = cocky . current_token if token . blazon == PLUS : self . swallow ( PLUS ) elif token . type == MINUS : cocky . eat ( MINUS ) node = BinOp ( left = node , op = token , right = self . term ()) render node def parse ( cocky ): render self . expr () Permit's get over the process of an AST construction for some arithmetics expressions.
If y'all look at the parser code to a higher place y'all tin can meet that the way information technology builds nodes of an AST is that each BinOp node adopts the electric current value of the node variable as its left kid and the result of a call to a term or factor as its correct child, then it's effectively pushing down nodes to the left and the tree for the expression 1 +2 + 3 + four + v below is a skillful example of that. Here is a visual representation how the parser gradually builds an AST for the expression ane + two + 3 + four + v:
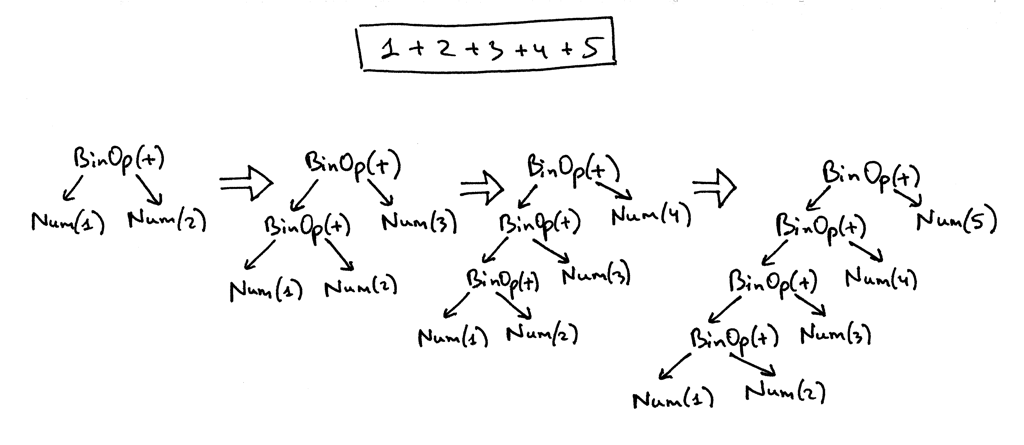
To help you visualize ASTs for different arithmetic expressions, I wrote a small utility that takes an arithmetics expression as its start argument and generates a DOT file that is then processed by the dot utility to really depict an AST for you (dot is function of the Graphviz bundle that you need to install to run the dot control). Here is a command and a generated AST image for the expression vii + iii * (x / (12 / (3 + ane) - one)):
$ python genastdot.py "vii + 3 * (10 / (12 / (three + 1) - 1))" > \ ast.dot && dot -Tpng -o ast.png ast.dot 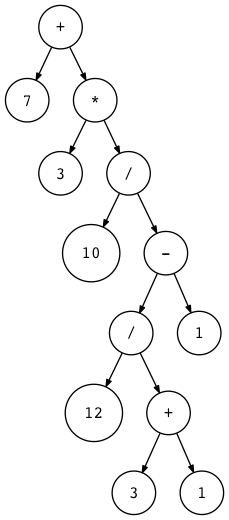
Information technology's worth your while to write some arithmetics expressions, manually draw ASTs for the expressions, and then verify them past generating AST images for the same expressions with the genastdot.py tool. That will help yous better understand how ASTs are synthetic by the parser for dissimilar arithmetic expressions.
Okay, here is an AST for the expression ii * 7 + 3:
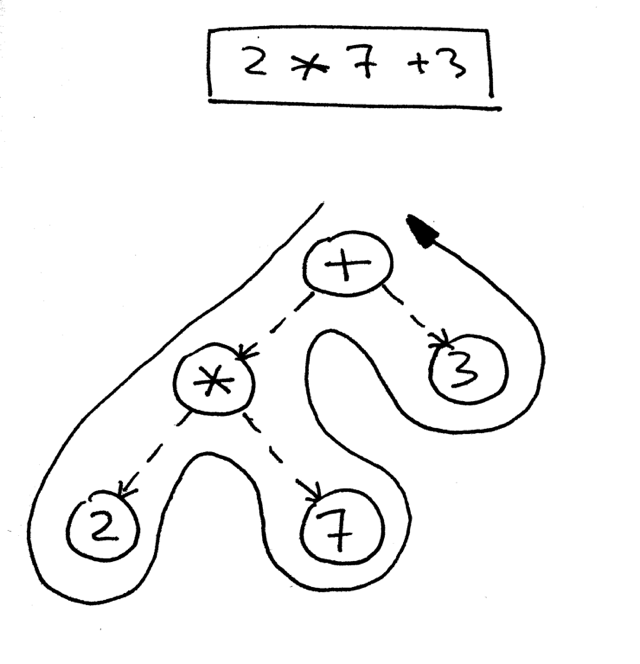
How practice you navigate the tree to properly evaluate the expression represented by that tree? You lot practise that by using a postorder traversal - a special case of depth-first traversal - which starts at the root node and recursively visits the children of each node from left to right. The postorder traversal visits nodes as far away from the root as fast equally it tin can.
Hither is a pseudo code for the postorder traversal where <<postorder actions>> is a placeholder for actions similar addition, subtraction, multiplication, or division for a BinOp node or a simpler activeness like returning the integer value of a Num node:

The reason we're going to apply a postorder traversal for our interpreter is that start, we need to evaluate interior nodes lower in the tree because they represent operators with higher precedence and second, we need to evaluate operands of an operator before applying the operator to those operands. In the picture beneath, you lot tin can see that with postorder traversal nosotros first evaluate the expression 2 * seven and only after that we evaluate fourteen + iii, which gives us the right result, 17:
For the sake of abyss, I'll mention that at that place are iii types of depth-first traversal: preorder traversal, inorder traversal, and postorder traversal. The name of the traversal method comes from the place where yous put deportment in the visitation code:

Sometimes yous might have to execute certain actions at all those points (preorder, inorder, and postorder). You'll see some examples of that in the source code repository for this article.
Okay, let'south write some code to visit and interpret the abstract syntax trees built by our parser, shall we?
Here is the source code that implements the Visitor pattern:
course NodeVisitor ( object ): def visit ( cocky , node ): method_name = 'visit_' + type ( node ) . __name__ visitor = getattr ( self , method_name , self . generic_visit ) return visitor ( node ) def generic_visit ( cocky , node ): heighten Exception ( 'No visit_{} method' . format ( type ( node ) . __name__ )) And here is the source lawmaking of our Interpreter grade that inherits from the NodeVisitor class and implements different methods that have the form visit_NodeType, where NodeType is replaced with the node'south class name similar BinOp, Num and and so on:
course Interpreter ( NodeVisitor ): def __init__ ( self , parser ): cocky . parser = parser def visit_BinOp ( self , node ): if node . op . type == PLUS : return self . visit ( node . left ) + self . visit ( node . right ) elif node . op . blazon == MINUS : return self . visit ( node . left ) - self . visit ( node . right ) elif node . op . type == MUL : render self . visit ( node . left ) * cocky . visit ( node . correct ) elif node . op . type == DIV : render self . visit ( node . left ) / self . visit ( node . right ) def visit_Num ( self , node ): return node . value There are ii interesting things about the code that are worth mentioning here: Get-go, the visitor code that manipulates AST nodes is decoupled from the AST nodes themselves. You can see that none of the AST node classes (BinOp and Num) provide any code to manipulate the data stored in those nodes. That logic is encapsulated in the Interpreter form that implements the NodeVisitor grade.
Second, instead of a giant if statement in the NodeVisitor's visit method like this:
def visit ( node ): node_type = blazon ( node ) . __name__ if node_type == 'BinOp' : render self . visit_BinOp ( node ) elif node_type == 'Num' : return self . visit_Num ( node ) elif ... # ... or similar this:
def visit ( node ): if isinstance ( node , BinOp ): render cocky . visit_BinOp ( node ) elif isinstance ( node , Num ): render self . visit_Num ( node ) elif ... the NodeVisitor's visit method is very generic and dispatches calls to the appropriate method based on the node type passed to information technology. As I've mentioned before, in guild to make use of it, our interpreter inherits from the NodeVisitor class and implements necessary methods. And so if the type of a node passed to the visit method is BinOp, and so the visit method volition dispatch the phone call to the visit_BinOp method, and if the type of a node is Num, then the visit method volition acceleration the phone call to the visit_Num method, and so on.
Spend some time studying this approach (standard Python module ast uses the aforementioned machinery for node traversal) as nosotros will be extending our interpreter with many new visit_NodeType methods in the futurity.
The generic_visit method is a fallback that raises an exception to indicate that it encountered a node that the implementation class has no corresponding visit_NodeType method for.
Now, allow's manually build an AST for the expression 2 * 7 + 3 and pass it to our interpreter to come across the visit method in action to evaluate the expression. Here is how you tin practise it from the Python shell:
>>> from spi import Token , MUL , PLUS , INTEGER , Num , BinOp >>> >>> mul_token = Token ( MUL , '*' ) >>> plus_token = Token ( PLUS , '+' ) >>> mul_node = BinOp ( ... left = Num ( Token ( INTEGER , ii )), ... op = mul_token , ... right = Num ( Token ( INTEGER , vii )) ... ) >>> add_node = BinOp ( ... left = mul_node , ... op = plus_token , ... right = Num ( Token ( INTEGER , 3 )) ... ) >>> from spi import Interpreter >>> inter = Interpreter ( None ) >>> inter . visit ( add_node ) 17 As you lot tin can see, I passed the root of the expression tree to the visit method and that triggered traversal of the tree past dispatching calls to the correct methods of the Interpreter grade(visit_BinOp and visit_Num) and generating the result.
Okay, hither is the complete lawmaking of our new interpreter for your convenience:
""" SPI - Uncomplicated Pascal Interpreter """ ############################################################################### # # # LEXER # # # ############################################################################### # Token types # # EOF (stop-of-file) token is used to indicate that # there is no more than input left for lexical analysis INTEGER , PLUS , MINUS , MUL , DIV , LPAREN , RPAREN , EOF = ( 'INTEGER' , 'PLUS' , 'MINUS' , 'MUL' , 'DIV' , '(' , ')' , 'EOF' ) class Token ( object ): def __init__ ( self , type , value ): cocky . type = blazon self . value = value def __str__ ( cocky ): """Cord representation of the course instance. Examples: Token(INTEGER, 3) Token(PLUS, '+') Token(MUL, '*') """ return 'Token({type}, {value})' . format ( blazon = self . type , value = repr ( self . value ) ) def __repr__ ( self ): return cocky . __str__ () class Lexer ( object ): def __init__ ( self , text ): # customer string input, e.g. "4 + 2 * three - 6 / ii" cocky . text = text # self.pos is an alphabetize into self.text self . pos = 0 self . current_char = cocky . text [ self . pos ] def error ( cocky ): raise Exception ( 'Invalid grapheme' ) def accelerate ( self ): """Accelerate the `pos` pointer and set the `current_char` variable.""" self . pos += one if self . pos > len ( self . text ) - i : self . current_char = None # Indicates end of input else : self . current_char = self . text [ self . pos ] def skip_whitespace ( self ): while cocky . current_char is not None and self . current_char . isspace (): self . accelerate () def integer ( self ): """Return a (multidigit) integer consumed from the input.""" result = '' while self . current_char is not None and cocky . current_char . isdigit (): issue += self . current_char self . advance () return int ( result ) def get_next_token ( self ): """Lexical analyzer (likewise known as scanner or tokenizer) This method is responsible for breaking a sentence apart into tokens. One token at a time. """ while cocky . current_char is not None : if self . current_char . isspace (): self . skip_whitespace () continue if self . current_char . isdigit (): return Token ( INTEGER , cocky . integer ()) if self . current_char == '+' : self . accelerate () return Token ( PLUS , '+' ) if self . current_char == '-' : self . advance () return Token ( MINUS , '-' ) if self . current_char == '*' : cocky . accelerate () return Token ( MUL , '*' ) if self . current_char == '/' : self . advance () return Token ( DIV , '/' ) if self . current_char == '(' : self . advance () return Token ( LPAREN , '(' ) if self . current_char == ')' : cocky . advance () return Token ( RPAREN , ')' ) self . fault () render Token ( EOF , None ) ############################################################################### # # # PARSER # # # ############################################################################### class AST ( object ): pass class BinOp ( AST ): def __init__ ( self , left , op , correct ): self . left = left self . token = cocky . op = op self . right = right form Num ( AST ): def __init__ ( self , token ): self . token = token self . value = token . value class Parser ( object ): def __init__ ( self , lexer ): cocky . lexer = lexer # set current token to the showtime token taken from the input self . current_token = self . lexer . get_next_token () def error ( self ): heighten Exception ( 'Invalid syntax' ) def eat ( self , token_type ): # compare the electric current token type with the passed token # type and if they lucifer then "eat" the current token # and assign the adjacent token to the self.current_token, # otherwise raise an exception. if self . current_token . type == token_type : self . current_token = cocky . lexer . get_next_token () else : self . mistake () def factor ( cocky ): """cistron : INTEGER | LPAREN expr RPAREN""" token = self . current_token if token . blazon == INTEGER : self . eat ( INTEGER ) return Num ( token ) elif token . blazon == LPAREN : self . consume ( LPAREN ) node = self . expr () self . consume ( RPAREN ) return node def term ( self ): """term : factor ((MUL | DIV) factor)*""" node = self . factor () while self . current_token . blazon in ( MUL , DIV ): token = self . current_token if token . type == MUL : self . swallow ( MUL ) elif token . type == DIV : self . eat ( DIV ) node = BinOp ( left = node , op = token , right = self . cistron ()) return node def expr ( self ): """ expr : term ((PLUS | MINUS) term)* term : factor ((MUL | DIV) cistron)* factor : INTEGER | LPAREN expr RPAREN """ node = self . term () while self . current_token . type in ( PLUS , MINUS ): token = self . current_token if token . blazon == PLUS : self . eat ( PLUS ) elif token . type == MINUS : self . eat ( MINUS ) node = BinOp ( left = node , op = token , right = self . term ()) render node def parse ( self ): return self . expr () ############################################################################### # # # INTERPRETER # # # ############################################################################### class NodeVisitor ( object ): def visit ( self , node ): method_name = 'visit_' + type ( node ) . __name__ visitor = getattr ( self , method_name , self . generic_visit ) render visitor ( node ) def generic_visit ( self , node ): enhance Exception ( 'No visit_{} method' . format ( blazon ( node ) . __name__ )) class Interpreter ( NodeVisitor ): def __init__ ( self , parser ): self . parser = parser def visit_BinOp ( self , node ): if node . op . type == PLUS : return self . visit ( node . left ) + cocky . visit ( node . right ) elif node . op . type == MINUS : render self . visit ( node . left ) - cocky . visit ( node . right ) elif node . op . type == MUL : render self . visit ( node . left ) * self . visit ( node . right ) elif node . op . type == DIV : render self . visit ( node . left ) / cocky . visit ( node . right ) def visit_Num ( self , node ): return node . value def translate ( self ): tree = self . parser . parse () return cocky . visit ( tree ) def main (): while True : effort : endeavor : text = raw_input ( 'spi> ' ) except NameError : # Python3 text = input ( 'spi> ' ) except EOFError : break if non text : continue lexer = Lexer ( text ) parser = Parser ( lexer ) interpreter = Interpreter ( parser ) result = interpreter . translate () print ( effect ) if __name__ == '__main__' : main () Save the above lawmaking into the spi.py file or download it straight from GitHub. Try it out and come across for yourself that your new tree-based interpreter properly evaluates arithmetic expressions.
Here is a sample session:
$ python spi.py spi> 7 + 3 * ( 10 / ( 12 / ( three + 1 ) - 1 )) 22 spi> 7 + 3 * ( 10 / ( 12 / ( 3 + ane ) - 1 )) / ( two + 3 ) - five - three + ( eight ) 10 spi> 7 + ((( 3 + 2 ))) 12
Today you've learned about parse trees, ASTs, how to construct ASTs and how to traverse them to interpret the input represented past those ASTs. You've besides modified the parser and the interpreter and separate them apart. The electric current interface betwixt the lexer, parser, and the interpreter at present looks like this:
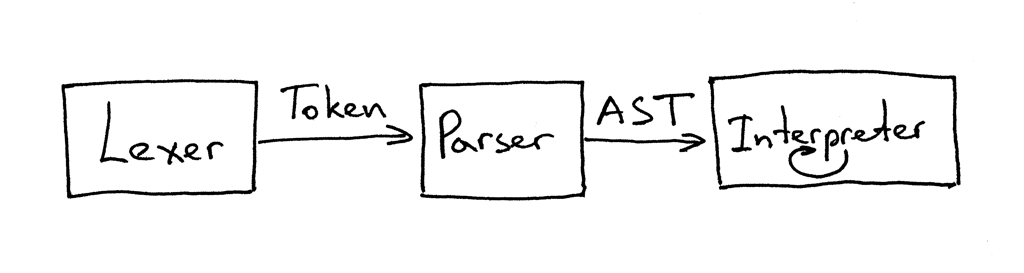
Yous can read that as "The parser gets tokens from the lexer and then returns the generated AST for the interpreter to traverse and translate the input."
That'south information technology for today, just before wrapping upward I'd like to talk briefly virtually recursive-descent parsers, namely just give them a definition considering I promised last time to talk about them in more detail. So here you become: a recursive-descent parser is a meridian-down parser that uses a set up of recursive procedures to process the input. Elevation-down reflects the fact that the parser begins by constructing the top node of the parse tree and then gradually constructs lower nodes.
And now it'southward time for exercises :)

- Write a translator (hint: node company) that takes as input an arithmetics expression and prints it out in postfix notation, too known every bit Reverse Polish Notation (RPN). For example, if the input to the translator is the expression (five + iii) * 12 / 3 than the output should be 5 3 + 12 * three /. See the respond hither but endeavor to solve it offset on your own.
- Write a translator (node visitor) that takes as input an arithmetic expression and prints it out in LISP style annotation, that is 2 + iii would become (+ ii 3) and (ii + 3 * 5) would get (+ 2 (* three 5)). Y'all can find the respond here but once again attempt to solve it outset before looking at the provided solution.
In the next article, nosotros'll add assignment and unary operators to our growing Pascal interpreter. Until then, take fun and see you soon.
P.S. I've also provided a Rust implementation of the interpreter that you can discover on GitHub. This is a way for me to learn Rust then keep in mind that the lawmaking might not exist "idiomatic" yet. Comments and suggestions as to how to make the code better are e'er welcome.
Hither is a list of books I recommend that will assistance y'all in your written report of interpreters and compilers:
-
Language Implementation Patterns: Create Your Own Domain-Specific and General Programming Languages (Pragmatic Programmers)
-
Writing Compilers and Interpreters: A Software Engineering Approach
-
Modern Compiler Implementation in Java
-
Modern Compiler Design
-
Compilers: Principles, Techniques, and Tools (second Edition)
If you want to get my newest manufactures in your inbox, and then enter your e-mail address below and click "Get Updates!"
All manufactures in this series:
- Let's Build A Uncomplicated Interpreter. Part 1.
- Let's Build A Elementary Interpreter. Part 2.
- Let's Build A Simple Interpreter. Part 3.
- Let'due south Build A Simple Interpreter. Office 4.
- Allow'south Build A Unproblematic Interpreter. Part v.
- Let's Build A Simple Interpreter. Part 6.
- Let's Build A Simple Interpreter. Office 7: Abstract Syntax Trees
- Let'south Build A Simple Interpreter. Part eight.
- Allow's Build A Simple Interpreter. Office 9.
- Let's Build A Elementary Interpreter. Part 10.
- Let's Build A Simple Interpreter. Part eleven.
- Let's Build A Uncomplicated Interpreter. Part 12.
- Let's Build A Simple Interpreter. Part xiii: Semantic Analysis
- Let's Build A Simple Interpreter. Office 14: Nested Scopes and a Source-to-Source Compiler
- Let's Build A Elementary Interpreter. Part 15.
- Let'southward Build A Unproblematic Interpreter. Part xvi: Recognizing Procedure Calls
- Permit'south Build A Unproblematic Interpreter. Part 17: Call Stack and Activation Records
- Let's Build A Elementary Interpreter. Part xviii: Executing Procedure Calls
- Let's Build A Elementary Interpreter. Function 19: Nested Procedure Calls
mcfaddentrock1953.blogspot.com
Source: https://ruslanspivak.com/lsbasi-part7/
0 Response to "How to Read a Syntax Tree While Loop"
Post a Comment